|
Efficient Ito diffusions on Riemannian manifolds |
|
Convergence properties of discrete curvature and a numerical treatment of the discrete Willmore functional Triply periodic minimal surfaces Small-time Asymptotics for the Heat Kernel on Finite Graphs and Manifolds Popular Matchings: Algorithmic Methods Popular Matchings in Graphs Piecewise Linear Vector Fields on Simplicial Surfaces On the Pentagram Map On Stochastic Dynamics of Polymer Chains Cheeger Inequalities Discrete Conformal Mappings of Triangle Meshes Discrete Exterior Calculus on Polygonal Meshes Stable Formulations of Discrete Elastic Rods A Curvature Measure on Smooth and Discrete Manifolds Solution of the Poisson Equation on Polyhedral Surfaces by Finite Elements with Quadratic Basis Functions Discrete Maximum Principle of Geometric Laplacians Computation of Geodesics in Shape Space using Modal Analysis Elastic Energy Regularization for Inverse Obstacle Problems Network elasticity of stiff rods connected by flexible linkers |
|
WS 23/24: Schulbezogene Angewandte Mathematik (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Inhalt: Lösung linearer Gleichungssysteme (Gauß, QR-Zerlegung, Cholesky); Banachscher Fixpunktsatz; Newtonverfahren; Graphentheorie; Numerische Integration; Polynominterpolation. |

|
WS 23/24: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
|
SS 2023: Seminar on Applied Funtional Analysis (2SE)
Die Termine sind im Stud.IP gelistet. Topics: The Banach fixed point theorem, the Lax-Milgram theorem, the Dirichlet principle, the Ritz method, the Brouwer fixed point theorem, convex sets and convex programming, game theory, spectral theory, Fourier transforms, semigroups and the heat equation, Feynman path integrals. |

|
SS 2023: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
|
WS 22/23: Introduction to Ricci Flow (4VL)
Die Termine sind im Stud.IP gelistet. We follow Peter Topping's lecture notes on Ricci flow. In particular, we cover 3-manifolds with positive Ricci curvature based on Hamilton’s program. |

|
WS 22/23: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
|
SS 2022: Introduction to Riemannian Geometry (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Topics include: abstract Riemannian manifolds, Levi-Civita connection, curvature, geodesics, Jacobi fields, Hadamard's Theorem, Theorem of Bonnet--Myers, Synge's Theorem. |

|
SS 2022: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 21/22: Introduction to geometry processing - Part I: Curves and Surfaces (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Topics include: differential geometry of planar and spatial curves, surfaces in Euclidean 3-space, Cartan's moving frames, first and second fundamental form, Gauss curvature, Theorema Egregium, Steiner's formulas, the Gauss-Bonnet theorem. |

|
WS 21/22: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
|
SS 2021: Numerische Mathematik II (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Inhalt: Polynominterpolation, trigonometrische Polynome und Splines, numerisch Integration mittels Newton-Cotes, Gauß-Quadratur und Romberg-Quadratur, Systeme von gewöhnlichen Differentialgleichungen, Runge-Kutta Verfahren, Grundlagen das Computer Aided Geometric Design (CAGD). |

|
SS 2021: Einführung in die Funktionalanalysis (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die lineare Funktionalanalysis gegeben. Themen: metrische Räume, normierte Räume, schwache Topologien und reflexive Räume, Hilberträume, Banachräume, lineare Operatoren, kompakte Operatoren, Fredholm-Operatoren, Spektralsatz. |

|
SS 2021: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 20/21: Einführung in die Graphentheorie (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die Graphentheorie gegeben. Themenauswahl: Eulersche und Hamiltonsche Graphen, Paarungen (Matchings), Ebene und planare Graphen, Färbungen, Netzwerke. Die Veranstaltung richtet sich an Studierende im B.Sc. Mathematik und Data Science. Sie ist inhaltlich auch für das Lehramt geeignet. |
|
WS 20/21: Numerische Mathematik I (4VL + 2UE)
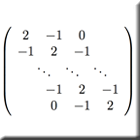
Die Termine sind im Stud.IP gelistet. Inhalt: Matrix- und Vektornormen; Banachscher Fixpunktsatz; direkte und iterative Lösungsverfahren für lineare Gleichungssysteme, Konvergenz iterativer Verfahren; Lösen nichtlinearer Gleichungssysteme mit dem Newtonverfahren; quadratische Ausgleichsprobleme zur Schätzung von Parametern aus Daten; numerische Berechnung von Eigenwerten und -vektoren von Matrizen. |

|
WS 20/21: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
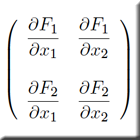
|
SS 2020: Mathematik für Informatiker II
(4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Inhalt: Grundbegriffe und grundlegende Eigenschaften von Stetigkeit und Differenzierbarkeit ein- und mehrdimensionaler Funktionen; Funktionenfolgen und -reihen, insbesondere Potenzreihen; Riemann-Integral und seine grundlegenden Eigenschaften. |

|
SS 2020: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 19/20: Seminar on Applied Funtional Analysis (2SE)
Die Termine sind im Stud.IP gelistet. Topics: The Banach fixed point theorem, the Lax-Milgram theorem, the Dirichlet principle, the Ritz method, the Brouwer fixed point theorem, convex sets and convex programming, game theory, spectral theory, Fourier transforms, semigroups and the heat equation, Feynman path integrals. |

|
WS 19/20: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
|
WS 19/20: Mathematik für Informatiker I (4VL + 2UE)
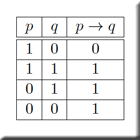
Die Termine sind im Stud.IP gelistet. Inhalt: Grundbegriffe der Logik; grundlegenden Eigenschaften von Vektorräumen, linearen Abbildungen und Matrizen sowie Eigenwerten und -vektoren; Lösen linearer Gleichungssysteme; Metriken und Normen; Konvergenz von Zahlenfolgen und -reihen; Definitionen und Eigenschaften von trigonometrischen, Exponential- und Logarithmusfunktionen. |

|
SS 2019: Seminar on Applied Funtional Analysis (2SE)
Die Termine sind im Stud.IP gelistet. Topics: Optimal control, the Banach fixed point theorem, the Lax-Milgram theorem, the Dirichlet principle, the Ritz method, the Brouwer and Schauder fixed point theorems, game theory, stochastic processes and functional analysis, semigroups and the heat equation, Feynman path integrals. |

|
SS 2019: Einführung in die Graphentheorie (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die Graphentheorie gegeben. Themenauswahl: Eulersche und Hamiltonsche Graphen, Paarungen (Matchings), Ebene und planare Graphen, Färbungen, Netzwerke. Die Veranstaltung richtet sich an Studierende im B.Sc. Mathematik und Data Science. Sie ist inhaltlich auch für das Lehramt geeignet. |

|
SS 2019: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
SS 2019: Einführung in die Funktionalanalysis (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die lineare Funktionalanalysis gegeben. Themen: metrische Räume, normierte Räume, schwache Topologien und reflexive Räume, Hilberträume, Banachräume, lineare Operatoren, kompakte Operatoren, Fredholm-Operatoren, Spektralsatz. |

|
WS 18/19: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
|
WS 18/19: Einführung in Partielle Differentialgleichungen (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die mathematischen Grundlagen linearer partieller Differentialgleichungen gegeben - von der elliptischen Theorie über parabolische Gleichungen bis hin zu hyperbolischen Systemen. Themenauswahl: Maximumprinzip, Schwache Lösungen, Sobolevräume, Regularität, Kompaktheit, Spektraltheorie, Energie Methoden, Separationsmethoden. |

|
WS 17/18: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 17/18: Introduction to geometry processing - Part III: Analysis on manifolds (4VL)
Die Termine sind im Stud.IP gelistet. This lecture provides an introduction to PDEs on Riemannian manfolds. Topics include: abstract Riemannian manifolds, the Levi-Civita connection, curvature, geodesics, Hodge decomposition, de Rham cohomology, Cheeger's inequalities (smooth), the heat kernel, the Chern-Gauss-Bonnet theorem. |

|
SS 2017: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
SS 2017: Introduction to geometry processing - Part II: Curves and Surfaces (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. This lecture provides an introduction to smooth and discrete surface theory. Topics include: differential geometry of planar and spatial curves, surfaces in Euclidean 3-space, Cartan's moving frames, first and second fundamental form, Gauss curvature, Theorema Egregium, Steiner's formulas, the Gauss-Bonnet theorem, alternating forms, Laplacians on forms, discrete Laplacians on discrete manifolds, discrete Hodge decomposition, Cheeger's inequalities (discrete). Tutors: Andy Sageman-Furnas and Friedrich Boes. |

|
WS 16/17: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 16/17: Introduction to geometry processing - Part I: Introduction to partial differential equations (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. This lecture offers an introduction to partial differential equations (PDEs). Topics include: harmonic functions, maximum principle, strong solutions of the Poisson problem, Green's function, energy methods, Sobolev spaces and weak solutions to elliptic PDEs, the Lax-Milgram theorem, discrete solutions to elliptic PDEs, the Riitz-Galerkin method, Delaunay triangulations, Rippa's theorem, the cotan Laplacian, discrete maximum principle, Fourier transformations, embedding theorems (Sobolev and Rellich-Kondrachov), Fredholm alternative, spectrum of the Laplacian. Tutors: Andy. Sageman-Furnas and Friedrich Boes. |

|
SS 2016: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
SS 2016: Numerische Mathematik II (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Inhalt: Polynominterpolation, trigonometrische Polynome und Splines, numerisch Integration mittels Newton-Cotes, Gauß-Quadratur und Romberg-Quadratur, Systeme von gewöhnlichen Differentialgleichungen, Runge-Kutta Verfahren, Grundlagen das Computer Aided Geometric Design (CAGD). |

|
WS 15/16: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 15/16: Numerische Mathematik I (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Inhalt: Matrix- und Vektornormen; Banachscher Fixpunktsatz; direkte und iterative Lösungsverfahren für lineare Gleichungssysteme, Konvergenz iterativer Verfahren; Lösen nichtlinearer Gleichungssysteme mit dem Newtonverfahren; quadratische Ausgleichsprobleme zur Schätzung von Parametern aus Daten; numerische Berechnung von Eigenwerten und -vektoren von Matrizen. |

|
SS 2015: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |
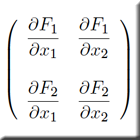
|
SS 2015: Mathematik für Informatiker II
(4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Inhalt: Grundbegriffe und grundlegende Eigenschaften von Stetigkeit und Differenzierbarkeit ein- und mehrdimensionaler Funktionen; Funktionenfolgen und -reihen, insbesondere Potenzreihen; Riemann-Integral und seine grundlegenden Eigenschaften. |

|
WS 14/15: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 14/15: Mathematik für Informatiker I
(4VL + 2UE)
Die Termine sind im Stud.IP gelistet. Inhalt: Grundbegriffe der Logik; grundlegenden Eigenschaften von Vektorräumen, linearen Abbildungen und Matrizen sowie Eigenwerten und -vektoren; Lösen linearer Gleichungssysteme; Metriken und Normen; Konvergenz von Zahlenfolgen und -reihen; Definitionen und Eigenschaften von trigonometrischen, Exponential- und Logarithmusfunktionen. |

|
SS 2014: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 13/14: Topologie und Datenanalyse (2SE)
Die Termine sind im Stud.IP gelistet. Wissenschaftler aller Couleur sammeln heutzutage enorme Datenmengen. Ein zentrales Problem ist deren robuste und effiziente Auswertung. Insbesondere sollen die entscheidenden qualitativen Informationen effizient ermittelt werden (oft aus verrauschten, hochdimensionalen Daten). Ziel des Seminars ist es, eine Einführung in das junge Gebiet der "Computational Topology" zu geben, die nötigen topologischen Grundlagen einzuführen (oder zu festigen), spezielle theoretische Konstruktionen kennen zu lernen, die dazugehörigen Algorithmen zu verstehen und einige konkrete Anwendungen anzuschauen. Dies ist eine gemeinsame Veranstaltung mit Thomas Schick. |

|
WS 13/14: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
SS 2013: Die Göttinger Sammlung mathematischer Modelle und Instrumente
(2SE)
Die Termine sind im Stud.IP gelistet. Warum hat man dem Apoll von Belvedere Linien ins Gesicht gezeichnet? Was haben Seifenhäute mit Minimalflächen zu tun? Wie kann man mechanisch integrieren? Diese und weitere Fragen werden wir mit Hilfe der Göttinger Sammlung mathematischer Modelle und Instrumente im mathematischen Institut in diesem Seminar beantworten. Auf den Spuren von Klein, Schoenflies und Hilbert werden wir die Exponate mit neuem Leben füllen. Seminarleitung: Julia Plehnert. |

|
SS 2013: Differential Geometry II (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In this second part of the differential geometry course, we plan to cover the following topics: introduction to Lie groups and Lie algebras, Riemannian manifolds, connections, parallel transport, introduction to hyperbolic geometry, Einstein manifolds. Tutor: Julia Plehnert. |

|
SS 2013: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 12/13: Differential Geometry of Curves and Surfaces (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In this classical introduction to differential geometry we cover the following topics: planar and spatial curves, convex curves, isoperimetric inequality, Steiner's formulas, surfaces in Euclidean 3-space, Cartan's moving frames, first and second fundamental form, Theorema Egregium, and more. Tutor: Henrik Schumacher. |

|
WS 12/13: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
SS 2012: Einführung in die Morsetheorie (2SE)
Die Termine sind im Stud.IP gelistet. Morsetheorie untersucht die Beziehung zwischen kritischen Punkten von Funktionen auf differenzierbaren Mannigfaltigkeiten und der Topologie des zu Grunde liegenden Raumes. Diese Beziehung hat weitreichende mathematische und physikalische Konsequenzen. Anhand von John Milnors Buch Morse Theory soll eine Einführung in die Morsetheorie gegeben werden. |

|
SS 2012: Oberseminar Discrete Differential Geomertry (2SE)
Die Termine sind im Stud.IP gelistet. Oberseminar der Arbeitsgruppe. |

|
WS 11/12: Diskrete Differentialgeometrie - Theorie und Anwendungen (2VL + 2UE)
Die Termine sind im Stud.IP gelistet. Diese zweistündige Vorlesung gibt eine Einführung in das junge Gebiet der Diskreten Differentialgeometrie. Themenauswahl: Topologische Charakterisierung von Flächen, Simpliziale Homologie und Kohomologie, diskrete Laplace-Operatoren, diskrete Krümmungen, Parametrisierung von Flächen, Simulation dünner Balken und Schalen. Tutorin: Clarisse Weischedel. |

|
SS 2011: Einführung in die Funktionalanalysis (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die lineare Funktionalanalysis gegeben. Themen: metrische Räume, normierte Räume, schwache Topologien und reflexive Räume, Hilberträume, Banachräume, lineare Operatoren, kompakte Operatoren, Fredholm-Operatoren, Spektralsatz. Tutoren: Peter Hintz, Henrik Schumacher und Benjamin Wacker. |

|
WS 10/11: Einführung in Partielle Differentialgleichungen (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die mathematischen Grundlagen linearer partieller Differentialgleichungen gegeben - von der elliptischen Theorie über parabolische Gleichungen bis hin zu hyperbolischen Systemen. Themenauswahl: Maximumprinzip, Schwache Lösungen, Sobolevräume, Regularität, Kompaktheit, Spektraltheorie, Energie Methoden, Separationsmethoden. Die VL ist eine gemeinsame Veranstaltung mit Gert Lube. Tutoren: Benjamin Wacker und Frank Werner. |

|
SS 2010: Differential Geometry II (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In this second part of the differential geometry course, we plan to cover the following topics: introduction to Lie groups and Lie algebras, Riemannian manifolds, connections, parallel transport, introduction to hyperbolic geometry, Einstein manifolds. This is a joint course with Chenchang Zhu. |

|
SS 2010: Topologie und Datenanalyse (2SE)
Die Termine sind im Stud.IP gelistet. Wissenschaftler aller Couleur sammeln heutzutage enorme Datenmengen. Ein zentrales Problem ist deren robuste und effiziente Auswertung. Insbesondere sollen die entscheidenden qualitativen Informationen effizient ermittelt werden (oft aus verrauschten, hochdimensionalen Daten). Ziel des Seminars ist es, eine Einführung in das junge Gebiet der "Computational Topology" zu geben, die nötigen topologischen Grundlagen einzuführen (oder zu festigen), spezielle theoretische Konstruktionen kennen zu lernen, die dazugehörigen Algorithmen zu verstehen und einige konkrete Anwendungen anzuschauen. Dies ist eine gemeinsame Veranstaltung mit Thomas Schick. |

|
WS 09/10: Differential Geometry I (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In this intoductory course to differential geometry, we cover the following topics: curves and surfaces in Euclidean 3-space, moving frames, first and second fundamental form, Theorema Egregium, abstract manifolds, vector fields, Frobenius theorem. This is a joint course with Chenchang Zhu. Tutors: Ulrich Bauer and Giorgio Trentinaglia. |
|
WS 09/10: Finite element exterior calculus, homological techniques, and applications to elasticity (2SE)
Die Termine sind im Stud.IP gelistet. The aim of this seminar is to study the recently developed Finite Element Exterior Calculus, which brings together ideas and techniques from finite element analysis, differential geometry, algebraic topology, and partial differential equations. This is a joint course with Thorsten Hohage and Gert Lube. [Poster] |

|
SS 2009: Einführung in Partielle Differentialgleichungen (4VL + 2UE)
Die Termine sind im Stud.IP gelistet. In dieser Vorlesung wird eine Einführung in die mathematischen Grundlagen linearer partieller Differentialgleichungen gegeben - von der elliptischen Theorie über parabolische Gleichungen bis hin zu hyperbolischen Systemen. Themenauswahl: Maximumprinzip, Schwache Lösungen, Sobolevräume, Regularität, Kompaktheit, Spektraltheorie, Energie Methoden, Separationsmethoden. Die VL ist eine gemeinsame Veranstaltung mit Gert Lube. Tutors: Alessio Quaglino and Lars Röhe. [Poster] |

|
WS 08/09: Diskrete Differentialgeometrie - Theorie und Anwendungen (2VL + 2SE)
Die Termine sind im Stud.IP gelistet. Diese zweistündige Vorlesung und das begleitende Seminar geben eine Einführung in das junge Gebiet der Diskreten Differentialgeometrie. Themenauswahl: diskrete Krümmungen, diskrete Differentialoperatoren, diskrete Morsetheorie, Parametrisierung von Netzen, Deformation von Netzen, Simulation diskreter Balken und Schalen. [Poster] |
Contact
Prof. Dr. Max Wardetzky
Institute for Numerical and
Applied Mathematics
University of Göttingen
Lotzestr. 16-18
37083 Göttingen, Germany
Tel. +49 (0)551 39-26778
Fax +49 (0)551 39-23944